Warning: this one might make your head hurt.

It’s a given that any client is going to want to change your designs in the middle of construction. If you’re lucky, it’s simple stuff like adding a door or changing the flooring from hardwood to pink polkadot vinyl. If you’re unlucky, it’s removing a critical column and redesigning the rest of the structure to take the new load.

The Comité de Padres de la Familia (the equivalent of the PTA) and the teachers have decided that the column in the center of the first-floor classrooms must go. I sympathize; it’s a distraction and will prevent some of the students from a clear view of the board, and would be totally unacceptable in an American classroom. But I put it there because I didn’t want to do anything structurally tricky, since the level of building expertise and quality control here is lower. Unfortunately for me, the mason told the teachers that they can just take the column out, and add a cross beam.

“Oh really?” I said, a bit annoyed and wondering how the mason had studied structural engineering while I was unawares.

“Sure!” he said, nodding. “We do it all the time. That’s how they built the church in the center of town, and it holds up a thousand people. No problem!” He then held up his tape measure, and stuck his thumb on a number. “If you’re worried, we’ll make it this thick.” Smiles all around.

This is one of those things that is basically impossible to explain to anyone here. Does the church’s beam have the same span? What steel did they use? How deep is it? Did they use high strength concrete? Is it going to survive the next earthquake? We’re not comparing apples to apples here. You can’t just wave your arm in the air and say, “Oh, it will be OK.” Not when the lives of the thirty students studying in the room below are at stake. Because when it all comes down to it, if the building collapses, I am the one who’s going to be guilty.

So, as most architects do, I spent the next evening worrying about it. It was pretty obvious that they were going to go forward with their mad plan; with other minor things, I’ve just let it go– these masons have been building stuff for decades, and the buildings still stand. But this main beam holds up everything. When faced with dilemmas like this, it’s time to do some calculations to put my mind at ease. For all you math and science nerds that heckled me a few posts back, this one’s for you.

The two (main) controlling design parameters in beam design are shear and moment. Imagine you have two chairs facing each other about three feet apart, and you set a strip of cardboard across the distance. Now place a weight in the middle. The cardboard will want to bend, and that is a manifestation of “moment”. If we could counter that, the bridge would not bend. This can be done by making the bridge shorter, or stronger (changing to a new material), or thicker.

If you were to place a second strip of cardboard on top of the first to make it thicker, it would be a little stronger. But as you add more weight, the two strips would have some slippage between themselves, more noticeable at the outside ends. That internal slippage is “shear”, and if it can be countered, the bridge will be stronger (such as by thoroughly gluing the two strips together).

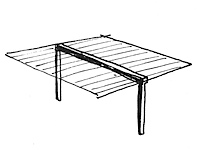
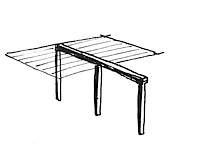
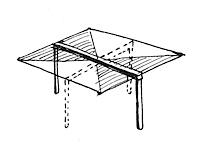
With most beams, moment is the controlling factor, but you need to check both. Let’s look at three different beams that relate to this building. For the following sketches: w= uniform load (mass per linear foot) and L= length. Per tradition, V is shear and M is moment. And now, some basic algebra as applied to statics.

	Full span beam, 30′ clear. Vmax= wL/2 Mmax= wL^2/8
	Beam with center column, original design, 15′ clear. Vmax= half of full span design (L is halved) Mmax= quarter of full span design (L is halved squared)
	Beam with center column replaced with crossing beam that carries half the load, 30′ clear. Vmax= half of full span design (.5L*.5 tributary width) Mmax= third of full span design ( .25wL*.33L-Vmax*.5L)

As you can see, the crossing beam design is the same as the center column design in terms of shear, but has a higher maximum moment. It’s not a LOT worse, but it could be enough to bring the building down. So now what? As luck would have it, there is also a cantilever at the far end of the beam: a little nub that sticks out past the column at one end, to carry the balcony. This creates a lot of moment too, and the beam is extra strong there to do the extra work. If we were designing airplanes, our beam would change shape along its length to minimize materials used; but this is just a building, and when you’re working with unskilled labor, it makes sense to just make the beam the same shape the entire length so it’s easier to build. And guess what? The moment at the cantilever is higher than any of the conditions above. So, to be strong enough to handle the cantilever, the beam is overdesigned enough in the center that the crossbeam idea will actually work. Whew!

There’s a saying, “God looks after dogs and fools.” In this case, it applies: the building will work, not because of churches or years of tradition or the mason’s promise or Mayan crossing-beam magic, but because of coincidence. And there is nothing all the science in the world can say about that.