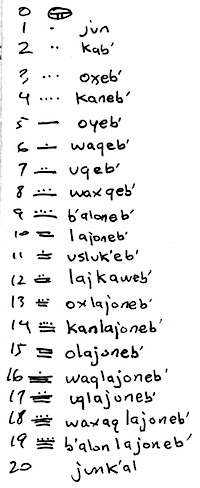WARNING: THIS MIGHT MAKE YOUR HEAD EXLPODE

While I was doing research for the Mayan teachers’ institute building, I had to look into Mayan mathematics. It’s a pretty cool field, and they teach an entire course on it at the institute. The Mayans were clever mathematicians, and invented the concept of “zero” before the time of Christ, centuries before it was used in Europe.

That’s fun for history buffs, but the math buffs will be interested to know that the Mayans use a vigesimal (base-20) counting system. Most of us count in decimal (base-10). You know: one, two, two, three, etc. but when you get to “ten”, it’s actually a one and a zero: 10. That means that you have one group of ten, and no more in the ones place. “12” means that you have one group of ten, plus two groups of one.

If you are a computer geek, you’ve probably been exposed to octal (base-8) or hexadecimal (base-16) counting. They require some math and head-bending to understand. For example, 55 in octal is 5 groups of 8 (=40) plus 5 groups of 1 (=5) for a total of 45 in decimal, the system we count in.

For systems that have more numbers than ours, they are trickier to represent. In hexadecimal, we use the first six letters of the alphabet to represent the numbers that just don’t exist in the decimal system. To count from one upwards, it’d be like this: 1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,10,11,12, and so forth. If we wanted to represent this same quantity 45 in hexadecimal (base-16), it would be 2D. That’s 2 groups of 16 (=32) plus D groups of 1 (=13) for a total of 45 in decimal.

The Mayan vigesimal (base-20) system is like hexadecimal, but more. Here are the numbers one through 20, as written, with their names in our local dialect (Q’anjob’al) –>

So if we wanted to write 45 in base-20, it would be 25. Two groups of 20 (=40) plus a group of 5. To write it in their markings, it would be two dots over a bar.

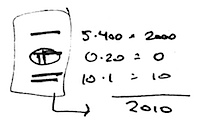Once we get to the third digit, it gets harder. The number “300” in our system means there are three in the hundreds place, none in the tens place, and none in the ones place. That first digit represents ten (the counting system) raised to the second power: hundreds. The same holds true for the other systems; in base-20, the first of the three digits is twenty raised to the second power: groups of 400. Soooo… to write our year “2010” in Mayan markings would be this.

Now lets bring this story full circle. A few days ago I was admiring our little Mayan sculpture, and I noticed it had a number written on the back- ./ ./// ./ What does it mean? A secret code? The day it was made? Let’s work it out: it’s 6×400 + 16×20 + 6×1 = 2726. Well, that was anticlimactic. Maybe that number holds some significance in the Mayan long-count calender? But now my head hurts, so the answer will have to wait for another day.